Zeros of Polynomial Functions
| Topic Review on "Title": |
Root:
A root is any real or complex number a where a polynomial takes the value 0.
Multiplicity of a Root:
The multiplicity of a root 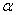 of a polynomial f(x) has multiplicity m if of a polynomial f(x) has multiplicity m if 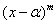 divides f(x) and divides f(x) and 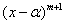 does not divide f(x). does not divide f(x).
Rolle’s Theorem:
Let f(x) be a polynomial and a and b are two numbers such that a<b and f(a)f(b)<0, then there is number c such that a<c<b and f(c)=0.
Descartes Rule:
The number of positive roots of 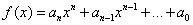 is at most the number of sign changes of its coefficients. is at most the number of sign changes of its coefficients.
Irreducible Polynomials:
Irreducible Polynomials are polynomials which cannot be factored (as a product of polynomials with real coefficients and of positive degree).
The fundamental theorem of algebra:
Let f(x) be a polynomial with real coefficients of degree n, then f(x) has exactly n complex roots 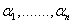 . If . If 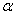 is a root, then its conjugate is also a root. is a root, then its conjugate is also a root.
Least Squares Principle:
Let f(x) be a polynomial of degree n minimizing:
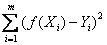 where where 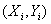 are the data and m is (much) bigger than n. Then f(x) is unique and it is the least squares regression polynomial. are the data and m is (much) bigger than n. Then f(x) is unique and it is the least squares regression polynomial.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial shows the basic definitions of the zeros of polynomial functions. Quadratic and cubic polynomials are presented with the use of graphs and the quadratic equation. The nature of roots is shown through the examples in this tutorial.
Polynomials of higher degree are shown with the use of the rational test, and Rolle’s Theorem. The roots and factoring polynomials are mentioned using theorems such as the irreducibility criterion and the fundamental theorem of algebra. Finally, an introduction to mathematical modeling is presented with the least squares principles and the regression model.
|
| Tutorial Features: |
Specific Tutorial Features:
• Examples showing how the roots of polynomials are found in some cases.
• Graphical representation of the regression and least squares principles to emphasize the theory of mathematical modeling.
Series Features:
• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
Basic definitions of the zeros of polynomial functions
Quadratic and Cubic Polynomials
Polynomials of higher degree
Rolle’s Theorem
The Rational Root Test
Descartes Rule
Roots and Factoring
Irreducibility criterion
The Fundamental Theorem of Algebra
Mathematical Modeling
Regression Principle
Least Squares Principle |
See all 24 lessons in College Algebra, including concept tutorials, problem drills and cheat sheets:
Teach Yourself College Algebra Visually in 24 Hours |



