Definition of a matrix:
Any 2-dimensional array of real or complex numbers.
Square matrix:
A matrix of type 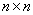 .
.
Diagonal:
The entries of a square matrix in the i-th line and i-th column (same index i), for some i.
Identity matrix:
A square matrix with 1’s on the diagonal and 0’s off the diagonal.
Zero matrix:
Any matrix (of any type), with only zero entries.
Definition of a 2-dimensional matrix:
We define of a 2-dimensional matrix as: 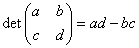 .
.
Definition of the rank of a matrix:
The rank of a matrix A is the greatest n such that A has a square sub-matrix of type nxn with determinant not equal to zero.
Definition of an invertible matrix:
We say a square matrix A is invertible if there exits a (square) matrix B such that AB=BA=identity matrix.
Cramer’s Rule:
If A is a square matrix, then the equation AV=w has a unique solution if and only if 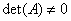 and the solution is
and the solution is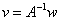 .
.



