Rational Functions
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial describes rational functions and their properties. The domain of rational functions is described with the use of horizontal and vertical asymptotes. The degrees of the two functions composing of a rational function are important to find the asymptotes of rational functions.
This tutorial describes the operation of rational functions with the use of examples. A rational function can be simplified by factoring the numerator function of rational functions and the denominator function of rational functions. Solving rational equations involves comparing the degrees and evaluating both functions so simplification can be achieved as much as possible.
|
| Tutorial Features: |
Specific Tutorial Features:
• Rational functions are reduced using simplification techniques.
• The asymptotes of rational functions are shown in some of the examples.
Series Features:
• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
Rational functions and their basic definitions
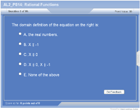
The domain of rational functions
Rational functions and their asymptotes
Formulas
The operations of rational functions
Simple rational functions
Simplification of rational functions
Polynomial equations
Polynomial equations and their solutions
|
See all 24 lessons in High School Algebra 2, including concept tutorials, problem drills and cheat sheets:
Teach Yourself High School Algebra 2 Visually in 24 Hours |



