The Normal Distribution
| Topic Review on "Title": |
Normal Distribution: describes a set of observations whose graph is symmetric and unimodal.
Normal Curve: is a special density curve that characterizes the normal distribution.
Parameters: numbers that help specify the model. For the normal distribution, the parameters are µ for the mean and σ for the standard deviation, written as N(µ, σ) .
Z-Score: standardized value of an observation that measures its distance from the mean.
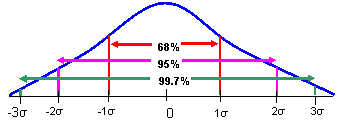
68-95-99.7 Rule: A sometimes termed the empirical rule, states that, in the Normal model: 68% of the observations in a distribution fall within 1 standard deviation of the mean, 95% of the observations in the distribution fall within 2 standard deviations of the mean, and 99.7% of the observations in the distribution fall within three standard deviations of the mean.
- Normal quantile plot: A graph used to verify the normality of a distribution.
- Standardize observations in order to compare values with different units.
- z-score = (x - μ)/ σ
- The z-score has no units.
- The z-score is an indication of how unusual a value is by how far away from the mean it is.
- Standardizing shifts the mean to zero and standard deviation to 1.
- Standardizing data does not change the shape of the graph.
- When working problems involving z-score and the 68-95-99.7 rule…draw a picture!
- x = any given observation
- σ =standard deviation
- μ = mean
- 68-95-99.7 Rule Used for finding the areas within a normal distribution.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial detailing normal distribution – describes a set of observations whose graph is
symmetric and unimodal. Many important concepts such as why and how data values are standardized, how to use z-scores to calculate area under the normal curve, how to use the 68-95-99.7 Rule, how to calculate z-score based on given information and to identify normal distributions by their normal quantile plot are all clearly demonstrated.
|
| Tutorial Features: |
Specific Tutorial Features:
- Step by step examples showing 68-95-99.7 rule is shown in this tutorial.
- Examples displaying how to find the z-score are presented with the use of graphs.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Normal Distribution
- Normal Curve
- Parameters
- Z-Score
- 68-95-99.7 Rule
- Normal quantile plot
- z-score
- Standardizing
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



