Probability
| Topic Review on "Title": |
- The role of probability: probability can be considered as a tool for statistics. Because probability deals with phenomenon exhibiting uncertainty
- Experiment: is a process which results in outcomes which occur unpredictably.
- Sample space: of an experiment is a set S of the outcomes.
- A simple event: is the outcome that is observed on a single repetition of the experiment.
- Event: is a collection of a sample space.
- Independent events: two events, A and B, are independent if the fact that A occurs does not affect the probability of B occurring.
- Conditional probability: the probability that one event occurs given that another has occurred is called conditional probability.
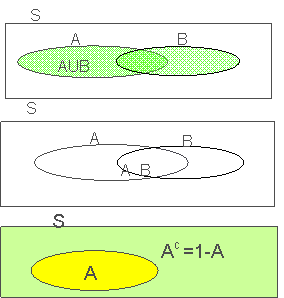
- The Union of events A and B is AUB
- The Intersection of events A and B is A∩B
- The Complement of event A is Ac=1-A
- Discrete probability distribution:
- Continuous probability distribution:
- p(x) > 0 for all x
- The total area under the curve is equal to 1.
- Checking for Independence:
- A and B are independent events, if P(A∩B)=P(A)·P(B)
- A and B are dependent events, if P(A∩B)≠P(A)·P(B)
- Two mutually exclusive events A and B:
- P(A|B)=0 or P(B|A)=0
- P(A∩B)=0
- P(AUB)=P(A)+P(B)
- A and B are dependent
- Two Independent events A and B:
- P(A∩B)=P(A)P(B)
- P(AUB)=P(A)+P(B)-P(A∩B)=P(A)+P(B)-P(A)P(B)
- The formula for conditional probability is:
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
Probability is widely used to support applications in biology, physics, psychology, and business, etc. Probability can help you to evaluate how reliable is your conclusions about the population from your sample information. This tutorial defines the properties of probability and provides many detailed illustrative examples.
The probability you will learn from this tutorial will be like a tool for statistics because probability deals with phenomenon exhibiting uncertainty.
|
| Tutorial Features: |
Specific Tutorial Features:
- Examples to illustrate the properties and applications of probability.
- Animated diagrams to actually show the relationship between dependent and independent events
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- The role of probability and probability rules
- Events and the sample space
- Event relations
- Dependent and independent events
- Conditional probability
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



