Binomial Distribution
| Topic Review on "Title": |
- Bernoulli trial: is an experiment whose outcome is random and can be either of two possible outcomes, "success" and “failure.”
- Independent trials: the outcome from one trial has no effect on the outcome to be obtained from any other trial.
- Binomial Experiment: 1) n independent 2) each trial result in only two outcomes: success and failure. 3) P(success)= p, is constant.
- Bernoulli distribution:
- Mean=px(1)+qx(0)=p
- Variance=pq
- Binomial distribution:
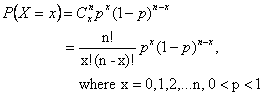
- Mean=np
- Variance=npq=np(1-p)
- Definition of a Binomial distribution:
- n independent trials
- each trial result in only success and failure.
- p, is constant.
- Normal Approximation to Binomial Distribution
As n approaches ∞ while p remains fixed, the following distribution approaches the normal distribution with mean 0 and variance
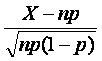
- Poisson approximation to Binomial Distribution
As n approaches ∞ and p approaches 0 while np remains fixed at λ > 0 or at least np approaches λ > 0,
Then the Binomial(n, p) distribution approaches the Poisson distribution with expected value λ.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
By completing this course, you will learn about binomial distribution, including Bernoulli distribution, binomial distribution and approximation of binomial distribution.
A Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, “success” and “failure.” This tutorial provides diagram which shows you the relationship between Bernoulli and binomial distribution.
Many practical and easy-to-understand examples are used to illustrate how to decide whether an experiment belong to binomial experiment or not and how to compute their related properties.
|
| Tutorial Features: |
Specific Tutorial Features:
- Examples showing the relationship between Bernoulli distribution and Binomial distribution, how to decide a binomial distribution etc.
- Examples with step by step assistance to solve problems relating how to use Poisson and normal distribution to approximate Binomial distribution.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Bernoulli trial
- Independent trials
- Binomial experiment
- Bernoulli distribution
- Binomial distribution
- Definition of a binomial distribution
- Poisson approximation to Binomial Distribution
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



