Geometric Distributions
| Topic Review on "Title": |
- Geometric distribution: refers to the probability of the number of times needed to do something until getting a desired result.
- Geometric Random Variables: is an example of a waiting time problem, that is, we wait until a certain event occurs. The number of Bernoulli trials which must be conducted before a trial results in a success.
- Geometric sequence: a sequence of numbers in which the (n+1)th number is a multiple of the nth number. P(X = n+1) is a multiple of P(X = n).
- Geometric distribution can be either one of the following:
- the probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set { 1, 2, 3, ...},
- or, the probability distribution of the number Y = X − 1 of failures before the first success, supported on the set { 0, 1, 2, 3, ... }.
- If the probability of success on each trial is p,
- then the probability that k trials are needed to get one success is either
- P(X=k)=(1-p)k-1p for k = 1, 2, 3, ...., or
- P(X=k)=(1-p)kp for k = 0, 1, 2, 3, ....
- Mean and variance:
- E(X)= 1/p
- Var(X)=(1-p)/p2
- Definition of a geometric experiment:
- Each observation falls into one of two categories, either “success” or “failure.”
- The probability of a success, call it p, is the same for each observation
- The observations are all independent (this allows us to multiply probabilities).
- The variable of interest is the number of trials required to obtain the first success.
- Comparison with other distributions:
- In the binomial distribution we have fixed number of trials and a variable number of successes
- In the geometric distribution we wait for a single success, but the number of trials is variable.
- The geometric random variable was the case of n=1 in negative binomial (NB).
- NB is the sum of Geometric distribution.
- If Y1,...,Yr are independent geometrically distributed variables with parameter p, then
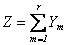 - Follows a negative binomial distribution with parameters r and p.
- Memoryless property:
- The geometric distribution is the only discrete memoryless random distribution.
- It is a discrete analog of the exponential distribution.
- If you intend to repeat an experiment until the first success, Then, given that the first success has not yet occurred,
- The conditional probability distribution of the number of additional trials does not depend on how many failures have been observed.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
Geometric distribution refers to the probability of the number of times needed to do something until getting a desired result. For instance, how many times will I throw a coin until it lands on a head? This belongs to geometric distribution.
By completing this course, you will learn about the geometric distribution, including introduction, geometric experiment, geometric random variable, comparison and relationship with other distributions and memoryless property.
|
| Tutorial Features: |
Specific Tutorial Features:
- Animated examples are shown as to how to calculate the probability of geometric distribution.
- Step by step explanation of the how to determine whether an experiment is geometric is shown in a couple of examples.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Geometric distribution
- Geometric random variables
- Geometric sequence
- Geometric experiment
- Comparison with other distributions
- Memoryless property
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



