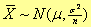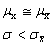
Normal Population (Data): If data are normally distributed with mean m and standard deviation s, and random samples of size n are taken,
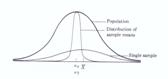
Then the sampling distribution of the sample means is also normally distributed.
The mean of all of the sample means is m.
The standard deviation of the sample means is s/√n
Non-Normal Population (Data): Even if data are not normally distributed, as long as you take “large enough” samples, the sample averages will at least be approximately normally distributed.
Mean of sample averages is still m
Standard error of sample averages is still s/√n
In general, “large enough” means more than 30 measurements.
Central Limit Theorem: even if data are not normally distributed, as long as you take “large enough” samples, the sample averages will at least be approximately normally distributed.
Mean of sample averages is still m
Standard error of sample averages is still s/√n
In general, “large enough” means more than 30 measurements.