Confidence Estimation
| Topic Review on "Title": |
Confidence Interval (CI) for a population parameter is:
An interval between two numbers with an associated probability p which is generated from a random sample of an underlying population,
Such that if the sampling was repeated numerous times and the confidence interval recalculated from each sample according to the same method,
A proportion p of the confidence intervals would contain the population parameter in question. Take an SRS of size n from a large population that contains a proportion parameter p of successes.
Let π be the sample proportion of successes. If the sample is large enough, then.
The sampling distribution of π is approximately normal.
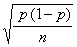
The mean of the sampling distribution is p.
The standard deviation of the sampling distribution is:
Formula for CI
zα/2 is called the critical value of the normal distribution at α level.
A table on next slide will gives you zα/2 for a particular level of confidence
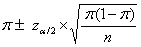
Commonly used values of za/2 |
Confidence level |
|
|
100(1-a) |
a |
a/2 |
za/2 |
90% |
.10 |
.05 |
1.65 |
95% |
.05 |
.025 |
1.96 |
99% |
.01 |
.005 |
2.58 |
CI for t-distribution
Small sample size population means
When creating a Confidence interval around m for a small sample we use (the df for ta/2 is n-1)
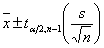
Assumption: random sample and population is approximately normally distributed
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial shows the principal concepts of confidence estimation. In statistics, interval estimation is the use of sample data to calculate an interval of possible (or probable) values of an unknown population parameter. The most prevalent forms of interval estimation are
confidence intervals.
By completing this course, you will learn about the confidence estimation, including confidence intervals, confidence intervals for population proportions, confidence intervals for the difference between two population proportions, confidence interval for population means, confidence intervals for the difference between two population means and small sample size confidence interval for population means
|
| Tutorial Features: |
Specific Tutorial Features:
- Several example problems with step by step illustrations of calculating confidence intervals are presented.
- Confidence intervals for the difference between two population proportions, and two population means are given for detailed explanation on how to calculate confidence intervals.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Confidence Intervals
- Confidence Intervals for population proportions
- Confidence Intervals for the difference between two population
- proportions
- Confidence Interval for population means
- Confidence Intervals for the difference between two population means
- Small Sample Size Confidence Interval for population means
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



