Chi-square tests
| Topic Review on "Title": |
Characteristics of Multinomial Experiments
- n identical trials in the multinomial experiments.
- The result of each trial will fall in one of k categories.
- pi = Prob( the result falls into category i on a single trial))
- pi = constant,
- p1+p2 +…+ pk = 1.
- Independent trials.
- O1, O2 ,… Ok = the number of outcomes in each category,
- O1 + O2 +… + Ok = n.
Characteristics of Binomial Experiments
- Only two categories (k=2): success and failure
- So it’s a special case of the multinomial experiment.
- p1 =p and p2 =1-p=q
- O1 =x and O2=n-x
Pearson’s Chi-Square Test
- Through samples, we want to test if our hypothesis (usually it is our unconfirmed idea about the values of the pi) is correct.
- The expected number of times that outcome i will occur is Ei = npi.
- Compare Ei with observed cell counts, Oi,
- If they are too far from what we hypothesize under H0, it’s very likely that H0 will be rejected.
- Assumptions for Pearson’s Chi-Square:
- Oi, i=1,…,k must satisfy the conditions of a multinomial experiment, or
- Row or column total fixed thus become a multinomial experiment.
- Ei≥5 , i=1,…,k.
- If Ei≥5 , i=1,…,k, then
- Increase sample size n. Then the chi-square distribution will be closer to the distribution of your test statistic X2.
- Combining one or more cells,
- Thus satisfying the assumption.
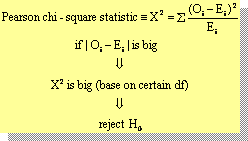
Degree of Freedom
- Degrees of freedom (df) : a way of keeping score.
- A data set has: n observations= n pieces of information.
- These pieces of information can be used either to estimate parameters or variance.
- It costs 1 df to estimate mean.
- The remaining (n-1) dfs are used to estimate variance.
- In a single sample with n observations, since estimating mean as a parameter cost you 1 df. That leaves n-1 dfs for the estimation of variance.
- In a table with k cell probabilities, we need to subtract 1df for the restriction of p1+p2 +…+ pk = 1 cost us 1 df.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial mentions chi-square tests and its different applications. Through samples, we want to test if our hypothesis (usually it is our unconfirmed idea about the values of the proportion in certain category) is correct and this is when we need to use Chi-square test.
By completing this course, you will learn about the chi square test including multinomial and binomial experiments, Chi square test, goodness of fit test, contingency tables, Chi square test of independence and multinomial population comparisons
|
| Tutorial Features: |
Specific Tutorial Features:
- Examples showing the goodness of fit test, contingency table, Chi-square test of independence are presented.
- Animated examples showing the comparisons of multinomial populations are presented.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Multinomial and Binomial Experiments
- Chi Square Test
- Goodness of Fit Test
- Contingency Tables
- Chi Square Test of Independence
- Multinomial Populations Comparisons
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



