Conics, Parabolas, Ellipses and Parabolas
| Topic Review on "Title": |
Definition of a parabola:
- A parabola is a set of all points in a plane that are equidistant from a given fixed point (the Focus) and a given straight line (the Directrix).
Different cases of parabolas:
- 1) With the vertex at the origin, the parabola opens in the positive x direction and has the equation
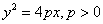 where vertex=(0,0) and focus is the point (p,0). where vertex=(0,0) and focus is the point (p,0).
- 2) With the vertex at the origin, the parabola opens in the negative x direction and has the equation
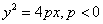 where vertex=(0,0) and focus is the point (p,0). where vertex=(0,0) and focus is the point (p,0).
- 3) With the vertex at the origin, the parabola opens in the positive y direction and has the equation
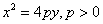 where vertex=(0,0) and focus is the point (0,p). where vertex=(0,0) and focus is the point (0,p).
- 4) With the vertex at the origin, the parabola opens in the negative y direction and has the equation
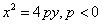 where vertex=(0,0) and focus is the point (0,p). where vertex=(0,0) and focus is the point (0,p).
Definition of an ellipse:
- An ellipse is a set of all points in a plane, whose distances from two fixed points (the foci) is a positive constant.
Different cases of ellipses:
- 1) The vertex is at the origin and the foci and the major axis are on the x-axis with the center at the origin and has the equation of the form
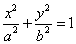 where the foci and the major axis are on the x-axis, the length of the major axis is 2a, the minor axis is on the y-axis, the length of minor axis equals to 2b and the center of the origin is at the origin (0,0). where the foci and the major axis are on the x-axis, the length of the major axis is 2a, the minor axis is on the y-axis, the length of minor axis equals to 2b and the center of the origin is at the origin (0,0).
- 2) The vertex is at the origin and the foci and the major axis are on the y-axis with the center at the origin and has the equation of the form
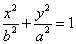 where the foci and the major axis are on the y-axis, the length of the major axis=2a, the minor axis is on the x-axis, length of the minor axis=2b and the center is at the origin (0,0). where the foci and the major axis are on the y-axis, the length of the major axis=2a, the minor axis is on the x-axis, length of the minor axis=2b and the center is at the origin (0,0).
Definition of a hyperbola:
- A hyperbola is a set of all points in a plane, the difference of whose distances from two fixed points (the foci) is a positive constant.
Different cases of hyperbolas:
- 1) The center is at the origin and the foci are on the x-axis and conjugate axis is the y-axis and has the equation of the form
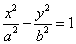 where the foci and the vertices are on the x-axis, the distance between the foci=2a, the conjugate axis is on the y-axis and the center is at the origin (0,0). where the foci and the vertices are on the x-axis, the distance between the foci=2a, the conjugate axis is on the y-axis and the center is at the origin (0,0).
- 2) The center is at the origin and the foci are on the y-axis and conjugate axis is the x-axis and has the equation of the form
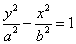 where the foci and the vertices are on the y-axis, the distance between the foci=2a, the conjugate axis is on the x-axis and the center is at the origin. where the foci and the vertices are on the y-axis, the distance between the foci=2a, the conjugate axis is on the x-axis and the center is at the origin.
Asymptotic Equations:
The equations of the asymptotes to the hyperbola 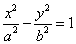 are as follows are as follows 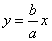 and and 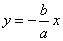 . .
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial introduces the conic sections and their different features. A general discussion of the brief history of conic sections and the formation of them is shown with graphical illustrations. Key conic sections such as a parabola and their properties are shown in the examples.
Ellipses and hyperbolas are defined with the help of graphs and the examples in this tutorial. Different scenarios where ellipses, hyperbolas change direction as far as their graphs are discussed in the sections of the tutorial. The foci and vertices of hyperbolas and ellipses are essential to the development of their graphs.
|
| Tutorial Features: |
Specific Tutorial Features:
• Step by step examples of the different aspects of the conic sections.
• “Completion of square” trick is used to bring the equations of the conic sections in standard form.
Series Features:
• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
Introduction to Conic Sections
A Brief History of the Conic Sections
Some applications
Parabola
Definition of a parabola
Different types of equations of a parabola
Ellipse
Definition of an ellipse
Relationship between foci and axes
Different types of equations of an ellipse
Hyperbola
Definition of a hyperbola
Relationship between foci and vertices
Mechanical vs. electromagnetic waves
Different types of equations of a hyperbola
Asymptotes of a hyperbola |
See all 24 lessons in Pre-Calculus, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Pre-Calculus Visually in 24 Hours |



