Infinite Sequences and Series
| Topic Review on "Title": |
The definition of infinite sequences:
An (infinite) sequence of real numbers is a function from the positive integers n into real numbers 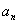 , , 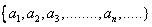
Limit of a sequence:
A sequence of real numbers 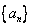 converges to the number converges to the number  if, for any if, for any 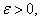 there is a positive integer there is a positive integer 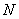 such that such that 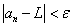 for any for any 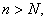 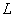 is called the limit of the sequence is called the limit of the sequence 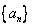 . .
Convergence of Cauchy sequences:
A sequence of real numbers converges if and only if it is a Cauchy sequence.
Subsequences of a sequence:
Subsequences are formed when we have a strictly increasing sequence of positive integers.
Convergence tests:
The comparison test, ratio test, root test, integral test and absolute/ conditional convergence test are the tests that are used to determine the convergence of series.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial specifically describes the concepts of infinite sequences and series. Examples are presented to with the basic operations and properties of infinite sequences. Applying some type of theorem to find the limit is important when dealing with sequences.
The properties of sequences with applications to approximation of limits are shown in the examples. The uniqueness and convergence of sequences need to be discussed before the concept of subsequences is defined. Sequences need to be bounded and monotonic so they can be classified as convergent sequences. Special sequences such as Cauchy sequences are also mentioned in this tutorial.
|
| Tutorial Features: |
Specific Tutorial Features:
• Graphs showing the convergence of sequences.
• Step by step analysis of the different types of convergence tests that can be used to determine is a series converges or not.
Series Features:
• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
Infinite sequences
Arithmetic and geometric progression
Definition of sequences
Recursive relations
Limit of a sequence
Divergence of sequences
Operations of a limit
Bounded and monotonic sequences
Definition of Cauchy sequences
Convergence of Cauchy sequences
Subsequences
Infinite series
Arithmetic sum
Geometric Series
Basic properties of series
Comparison test
Ratio, root, integral, p-series and alternating series test
|
See all 24 lessons in Pre-Calculus, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Pre-Calculus Visually in 24 Hours |



